Всем привет! Сегодня мы научим Ваш компьютер распознавать цифры.
Вы можете скачать уже готовый набор цифр, которые я рисовал в фотошопе или сделать его самому. И да, я совсем забыл про ноль.
Набор цифр в формате .BMP 30X30
Изображения имеют следующий формат имени: [ЦИФРА]_[ПОРЯДКОВЫЙ_НОМЕР]
Каждая цифра имеет 15 вариантов моего написания. Если сделать меньше вариантов, то модели будут сильно недообучаться.
Подготовка данных
Произведем импорт необходимых библиотек:
[python]
import numpy as np
import pandas as pd
from PIL import Image
from numpy import array
[/python]
Считаем значения пикселов для каждого изображения в Dataframe
[python]
df = pd.DataFrame();
# Обрабатываем изображение для каждой цифры от 1 до 9
for x in range(1, 10):
# Обрабатываем все 15 вариантов написания конкретной цифры
for y in range(1, 16):
imgName = str(x) + «_» + str(y) + «.bmp»;
img = Image.open(imgName)
arr=array(img) # массив arr теперь хранит значения яркостей для каждого пиксела
arr=np.append(arr, x) # добавляем в массив целевой признак — саму цифру
df_tmp = pd.DataFrame([arr.tolist()]) # преобразуем массив в DataFrame
df=df.append(df_tmp) # Добавляем строчку в итоговый DataFrame dataframe
df.head()
[/python]
Проименуем столбцы следующим образом:
- от 0 до 899 — номера пикселов (всего 900 для каждого изображения 30×30)
- target — для целевого признака, конкретной цифры
[python]
df=df.reset_index(drop=True)
labels = list()
for x in range(0, 901):
if(x < 900):
labels.append(str(x))
else:
labels.append(‘target’)
df.columns = labels
df.head(100)
[/python]
Дерево решений
Обучим дерево решений. Максимальная глубина дерева — 200.
[python]
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X = df.drop([‘target’], axis=1)
y = df[‘target’]
[/python]
[python]
X_train, X_test, y_train, y_test = train_test_split(X, y)
[/python]
[python]
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(max_depth=200)
tree.fit(X_train, y_train)
print(«Accuracy on train dataset: {:.2f}».format(tree.score(X_train, y_train)))
print(«Accuracy on test dataset: {:.2f}».format(tree.score(X_test, y_test)))
[/python]
Точность на тренировочной выборке — 100%
Точность на тестовой выборке — 94%
Проверим, как меняется точность на тестовой выборке в зависимости от параметра «Максимальная глубина дерева»
[python]
%matplotlib inline
import matplotlib.pyplot as plt
X_train, X_test, y_train, y_test = train_test_split(df.drop([‘target’], axis=1), df[‘target’], stratify=df[‘target’])
training_accuracy = []
test_accuracy = []
max_depth_settings = range(1, 25)
for max_depth in max_depth_settings:
# Строим модель
clf = DecisionTreeClassifier(max_depth=max_depth)
clf.fit(X_train, y_train)
# Записываем правильность на обучающем наборе
training_accuracy.append(clf.score(X_train, y_train))
# Записываем правильность на тестовом наборе
test_accuracy.append(clf.score(X_test, y_test))
plt.figure(figsize=(10, 10))
plt.plot(max_depth_settings, training_accuracy, label=»Accuracy on training data»)
plt.plot(max_depth_settings, test_accuracy, label=»Accuracy on test data»)
plt.ylabel(«Accuracy»)
plt.xlabel(«Max depth»)
plt.legend()
[/python]

Зависимость точности прогноза дерева решений от его глубины на обучающей и тестовой выборках
Как видно, увеличение глубины дерева после значения 5 не улучшает точность прогноза.
Метод ближайших соседей
Напомню, что дерево решений не требует нормализации данных, в отличие от метода ближайших соседей. Поэтому подготовим данные с помощью StandardScaler. Хотя, на самом деле, здесь это делать не обязательно, так как величины всех признаков измерены в одном масштабе от 0 до 255, но это скорее исключение, чем правило, поэтому произведем нормализацию.
[python]
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
X = df.drop([‘target’], axis=1)
y = df[‘target’]
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X.as_matrix())
[/python]
[python]
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y)
[/python]
[python]
from sklearn.neighbors import KNeighborsClassifier
clf = KNeighborsClassifier(n_neighbors=1)
clf.fit(X_train, y_train)
print(«Accuracy on train dataset: {:.2f}».format(clf.score(X_train, y_train)))
print(«Accuracy on test dataset: {:.2f}».format(clf.score(X_test, y_test)))
[/python]
Построим график зависимости точности прогноза на обучающей и тестовой выборках в зависимости от количества соседей.


Видно, что чем больше соседей учитывает алгоритм, тем менее точен прогноз. Несмотря на то, что Вам может показаться, что лучше всего брать количество соседей равное одному, то в большинстве задач это не так, так как при таком значении параметра алгоритм сильно переобучается.
Давайте теперь заставим модель указать, какое число нарисовано. Я нарисовал дополнительную цифру в файле 8_16.bmp
[python]
clf = KNeighborsClassifier(3)
clf.fit(X_train, y_train)
img = Image.open(«8_16.bmp»)
arr=array(img)
arr=arr.tolist()
arr=np.append(arr, 0)
arr=arr[:-1]
#print(arr)
X_new = np.array([arr])
prediction = clf.predict(X_new)
print(«Прогноз: {}».format(prediction))
[/python]
Модель правильно угадала число. Интересно, что если ввести количество соседей более 90, то моя модель путала восьмерку с двойкой. И это понятно, потому что 8 от 2 отличается только одной небольшой диагональной линией.
Линейные модели
Гребневая регрессия
Линейные модели хорошо работают на высокоразмерных данных и это как раз тот самый случай. Начнем сразу с гребневой регрессии, так как у нее есть параметр регуляризации:
[python]
from sklearn.linear_model import Ridge
ridge10 = Ridge(alpha=10).fit(X_train, y_train)
print(«Правильность на обучающем наборе: {:.2f}».format(ridge10.score(X_train, y_train)))
print(«Правильность на тестовом наборе: {:.2f}».format(ridge10.score(X_test, y_test)))
[/python]
Параметр регуляризации подберите сами.
Правильность на обучающем наборе: 1.00
Правильность на тестовом наборе: 0.96
Это очень хороший результат, учитывая, что линейные модели работают очень быстро, поэтому их без проблем можно применить к изображением с более высоким разрешением.
Лассо
[python]
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train, y_train)
print(«Правильность на обучающем наборе: {:.2f}».format(lasso.score(X_train, y_train)))
print(«Правильность на контрольном наборе: {:.2f}».format(lasso.score(X_test, y_test)))
print(«Количество использованных признаков: {}».format(np.sum(lasso.coef_ != 0)))
# Мы увеличиваем значение «max_iter»
# иначе модель выдаст предупреждение, что нужно увеличить max_iter
lasso001 = Lasso(alpha=0.01, max_iter=100000).fit(X_train, y_train)
print(«Правильность на обучающем наборе: {:.2f}».format(lasso001.score(X_train, y_train)))
print(«Правильность на тестовом наборе: {:.2f}».format(lasso001.score(X_test, y_test)))
print(«Количество использованных признаков: {}».format(np.sum(lasso001.coef_ != 0)))
lasso00001 = Lasso(alpha=0.0001, max_iter=100000).fit(X_train, y_train)
[/python]
Строим график значений коэффицентов для признаков
[python]
plt.figure(figsize=(7,7))
plt.plot(lasso.coef_,’s’,label=»Lasso alpha=1″)
plt.plot(lasso001.coef_, ‘^’, label=»Lasso alpha=0.01″)
plt.plot(lasso00001.coef_, ‘v’, label=»Lasso alpha=0.0001″)
plt.plot(ridge10.coef_, ‘o’, label=»Ridge regressions alpha=0.1″)
plt.legend(ncol=2, loc=(0, 1.05))
plt.ylim(-0.05, 0.05)
plt.xlabel(«Index of the coefficient»)
plt.ylabel(«Coefficient»)
[/python]
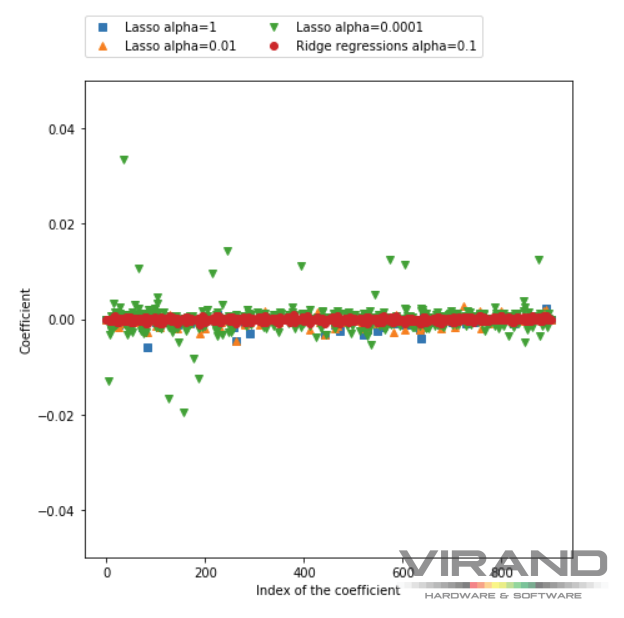
Коэффициенты при признаках лассо с разной регуляризацией
Данный график не очень информативен. Главная особенность лассо заключается в том, что она обнуляет коэффициенты неинформативных признаков. Логично предположить, что неинформативными в нашем случае являются пикселы по краям изображения. Проверим.

Обратите внимание, на значения признаков в районе 0, 30, 60, 90. Эти признаки соответствуют пикселам, расположенных по краям изображения. И, действительно, лассо обнулила значения этих признаков.
Нейронная сеть
Построим и обучим нейронную сеть с 40 входными переменными и 10 скрытыми слоями.
[python]
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(solver=’lbfgs’, random_state=0, hidden_layer_sizes=[40, 10], alpha=1)
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y)
mlp.fit(X_train, y_train)
print(«Accuracy on train data: {:.2f}»).format(mlp.score(X_train, y_train))
print(«Accuracy on test data: {:.2f}»).format(mlp.score(X_test, y_test))
[/python]
Точность на обучающей и тестовой выборках — 100%. Да, в таких задачах нейронным сетям нет равных. Однако, нейронные сети гораздо дольше обучаются и их сложно анализировать. Но все же попробуем. Построим теплокарту весов первого словия.
[python]
plt.figure(figsize=(10, 900))
plt.imshow(mlp.coefs_[0], interpolation=’none’, cmap=’magma’)
plt.yticks(range(900), labels)
plt.xlabel(«Columns of the matrix weights»)
plt.ylabel(«Input characteristic»)
plt.colorbar()
[/python]

Теплокарта весов первого слоя нейронной сети
Как видно, коэффиценты признаков, отвечающих за пикселы, расположенные по краям изображения здесь также являются неинформативными.


